Рассмотрим способы определения прогибов, углов поворота, моментов и поперечных сил в любом сечении балки жесткости при частичном загружении моста равномерной нагрузкой, как показано на комментируемом рисунке ниже. При таком загружении для величин 1′]; 1′]’; и Q необходимо получить уравнения для трех участков.
Если, исходя из уравнения (IV.l), написать три дифференциальных уравнения для трех участков, то при интегрировании возникает необходимость определить 12 произвольных постоянных. Для упрощения решения будем пользоваться уравнением (IV.4). Принимая жесткость балки ЕI постоянной, а нагрузку от собственного веса равномерной, примем очертания кабеля по квадратной параболе.
Учитывая, что
У»(х)= _}.L= —g- [2 Hg ,(Ь)

Непосредственное интегрирование этих уравнений так же вызывает трудности из-за необходимости определять шесть произвольных постоянных. Поэтому сделаем еще одно упрощение предположим, что функции М, Мп и Мш графически изображаются кривыми 0-1, 1-2 и 2-3 . Продлим кривую М а точки 1 до 1′ а точку 5 кривую Мп — до точки 4. Расстояние по вертикали между кривыми М! и Мп обозначим Mr, а между Мп ~ Мш – соответственно Мп видно, что ординаты функций МП и Мш можно определить, как разность соответствующих ординат:

Перед тем как начать рассмотрение этого раздела, считаем необходимым ознакомиться с содержанием раздела о колебаниях.
Частоты и формы изгибных колебаний висячего моста в значительной степени зависят от геометрических размеров закона изменения жесткости балки.
Для анализа этого вопроса рассмотрим случай, когда момент инерции балки изменяется па закону (VIII.21). Эти законы легко получить из выражения (VIII.21) при условия, что при x=lj4 и x=lj2 жесткость соответственно равна EIl14 и E1112.

В последнее время в висячих мостах стали применять такие системы, в которых кабель жестко соединен с балкой в середине пролета. Основная идея, породившая эту конструкцию, состоит в стремлении увеличить жесткость системы при несимметричном ее загружении временной нагрузкой. Расчет таких систем усложняется тем, что появляется еще одно лишнее неизвестное горизонтальное усилие, передающееся с кабеля на балку жесткости.
В указанной конструкции есть по существу, два самостоятельных кабеля, к которым подвешена балка. Основные расчетные уравнения, естественно усложняются. Однако применение ПК позволяет получать решение при различных загружениях моста временной нагрузкой.
Для вывода основных уравнений в предварительно была рассмотрена гибкая нить, у которой один конец имеет подвижную опору в вертикальном направлении.
Рассмотрим однопролетный мост с балкой постоянного сечения. При решении системы с балкой переменного сечения не возникает никаких затруднений. Различие будет состоять только в составлении матрицы упругих грузов. Методика расчета и все основные допущения остаются прежними. Величины перемещений и усилий, относящиеся к левой и правой частям, будем обозначать буквами и снабжать их индексами «л» И «п».
Между усилиями в подвесках и ординатами оси кабеля после деформации существует, следующая зависимость для левой половины
(V.57)
для правой половины
(V.58)
где Нл и Нп -величины распоров в левой и правой частях кабеля 11Л и llП — прогибы в левой и правой частях балки от загружения системы временной нагрузкой.
Введем обозначения:
НЛ+ Н!! =Н;
НЛ — НII = 6Н

В наши дни висячие мосты сооружаются различных типов, среди которых основное место занимают кабельные мосты, главными несущими элементами у которых являются гибкие кабели из высокопрочной металлической проволоки и балками жесткости. Такие мосты обладают большой прочностью и грузоподъёмностью, эти технологии успешно применяются, как для автомобильных мостов, так и для мостов через которые идёт железнодорожный транспорт.

Проблема собственных колебаний висячих мостов, как было сказано в первом разделе нашего сайта, решена сравнительно недавно.
Однако решение в основном проводилось для мостов с балкой жесткости постоянного сечения. Кроме того, в большинстве работ даны приближенные решения, в которых, как правило, не учтена динамическая добавка к распору, возникающая от сил инерции.

Для случая, когда балка жесткости имеет переменное сечение и учитывается динамический распор, нахождение частот и форм колебаний представляет собой сложную задачу, связанную с интегрированием сложных дифференциальных уравнений с переменными коэффициентами.
Вследствие того, что подобные задачи не решаются в замкнутом виде, приходится применять вариационные методы и вычислительные машины, современные компьютеры на базе 4 ядерных процессоров.
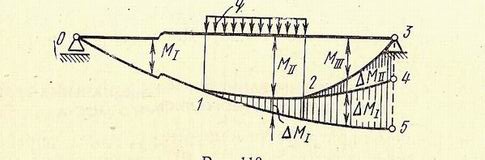
При изучении собственных колебаний висячего моста, так же как и при расчете на прочность, будем предполагать, что от действия постоянной нагрузки изгибающие моменты в балке жесткости равны нулю. Такое условие, как уже выяснилось ранее, можно обеспечить при навесной сборке, когда замыкание подвешенных к кабелю звеньев балки жесткости производится после того, как все работы па сборке пролетного строения полностью закончены.
Несмотря на то что балка жесткости будет иметь переменное сечение, мы будем предполагать, что масса погонного метра пролетного строения моста постоянна по всей длине. Такое допущение не является противоречивым. Дело в там, сто погонная масса складывается из массы всего пролетного строения, в которую входят массы проезжей части, настила, перил, покрытия проезжего полотна и т. д. Масса самой балки жёсткостти, хотя и является переменной, составляет незначительную часть от общей массы моста.
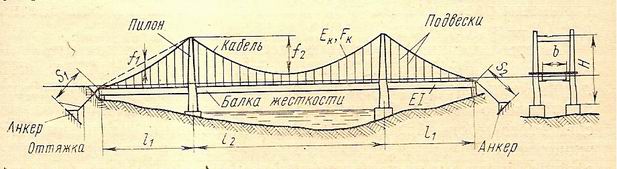
В расчетах на прочность мы считали, что задача относительно продольной оси моста является симметричной, т. е. нагрузка в поперечном направлении расположена симметрично. Эта позволило рассматривать один кабель и одну несущую балку как отдельную плоскую систему. В связи с этим все геометрические размеры — моменты инерции балки, площадь кабеля, а также силовые величины — распор, изгибающие моменты, постоянную и временную нагрузки — следует определять для половины моста. Поскольку изучение колебаний висячих мостов является пространственной задачей (например, при крутильных колебаниях), следует особо оговорить обозначения, принятые в настоящей главе. Будем обозначать g — интенсивность постоянной нагрузки, приходящейся на один кабель (т. е. для половины поперечного сечения моста);
Н g — распор от постоянной нагрузки в одном кабеле Е (х) и ЕяР — изгибная жесткость одной несущей балки в произвольном сечении и жесткость кабеля.
Принимая во внимание все вышеизложенные моменты и опираясь на предыдущие разделы сайта можно сделать вывод о Важности вычисления колебаний при инертности и инертных колебаниях, формулы инертных колебаний будут приводиться в следующих статьях нашего проекта.