ОДНОПРОЛЁТНЫЙ МОСТ (УПРАВЛЕНИЕ)

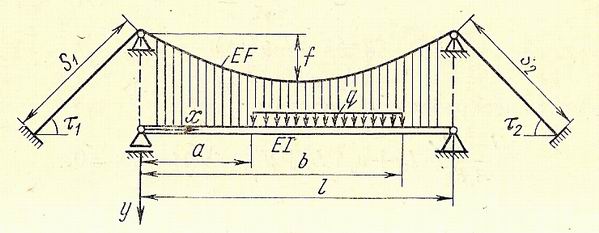
Рассмотрим способы определения прогибов, углов поворота, моментов и поперечных сил в любом сечении балки жесткости при частичном загружении моста равномерной нагрузкой, как показано на комментируемом рисунке ниже. При таком загружении для величин 1′]; 1′]’; и Q необходимо получить уравнения для трех участков.
Если, исходя из уравнения (IV.l), написать три дифференциальных уравнения для трех участков, то при интегрировании возникает необходимость определить 12 произвольных постоянных. Для упрощения решения будем пользоваться уравнением (IV.4). Принимая жесткость балки ЕI постоянной, а нагрузку от собственного веса равномерной, примем очертания кабеля по квадратной параболе.
Учитывая, что
У»(х)= _}.L= —g- [2 Hg ,(Ь)

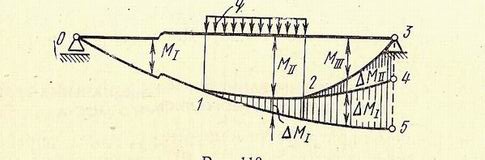
Непосредственное интегрирование этих уравнений так же вызывает трудности из-за необходимости определять шесть произвольных постоянных. Поэтому сделаем еще одно упрощение предположим, что функции М, Мп и Мш графически изображаются кривыми 0-1, 1-2 и 2-3 . Продлим кривую М а точки 1 до 1′ а точку 5 кривую Мп — до точки 4. Расстояние по вертикали между кривыми М! и Мп обозначим Mr, а между Мп ~ Мш – соответственно Мп видно, что ординаты функций МП и Мш можно определить, как разность соответствующих ординат:

MII (x)=MI(X)- АМ! (х);
Мш (х)=М! (х) — [АМ! (~)+ t-MII (х)].

Значения ординат функции L1MI и L1Мп определяются более просто, чем функции Мп и Мш. Вычтя уравнение (d) из (с), а уравнение ( е) из (d) и учтя равенства (f) и (g), получим дифференциальные уравнения для функций:
Остается определить постоянную величину Во. Для этой цели используем условие Мш (l) =0.