ОСНОВНЫЕ УРАВНЕНИЯ

Трудно вкратце выложить в Интернет, все сведения касающиеся этого раздела, но мы постарались и выложили основное, если что то не ясно не стесняйтесь пишите и задавайте вопросы.

В процессе деформации пролетного строения висячего моста определенные точки оси кабеля могут перемещаться как по вертикали, так и по горизонтали. Величины горизонтальных перемещений в сильной степени зависят от пологости кабеля. Для тех Случаев, когда f/l меньше или равно 1/10, горизонтальными перемещениями можно пренебречь и считать, что все подвески будут перемещаться толька ,по вертикали.
Поскольку расстояние между подвесками по сравнению с длиной пролета невелико, будем считать, что подвески сплошь заполняют пространство между балкой и кабелем. Примем гипотезу о не растяжимости подвесок. На основании сделанных допущений можно считать, что в каждом сечении вертикальные перемещения оси кабеля и балки будут одинаковыми. Обозначим эти перемещения, как и ранее, через N, интенсивнасть временной нагрузки — q, Т/М, постоянной — N, Т/М, распор в кабеле от постоянной нагрузки — Hg, а полной (от постоянной и временной нагрузок) — Н.
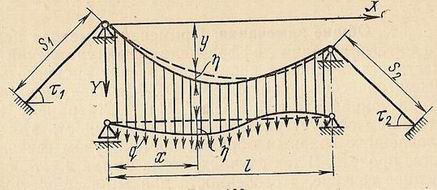
Рассмотрим вначале систему, на которой пунктиром показана балка, подвешенная к кабелю, очерченному по квадратной параболе, а сплошной линией изображены та же балка и кабель после деформации от временной нагрузки.
До загружения балки нагрузкой q она не пригибается, т. е. имеет место равенства

Суммарная интенсивная нагрузка в произвольном сечении балки, которую обозначим через q, после загружения временной нагрузкой qп будет определяться выражением

qn= — н [у (x)+’I’] (х))» -(g+q).

Дифференциальное уравнение для прогиба балки в соответствии с ,осями координат, имеет вид

[E!’I’]» (х))» = — qn=H [у (x)+’I’] (х)] 11 +(g+q).

Для ‘случая Е! =const с учетом равенства (а) получим дифференциальное уравнение прогибов

Н-Н q ‘IlIV(x)-а2’1l»(х)= g y’f(X)+_
Е/ ЕI где a=V ;.
Если учесть, что м (х)= -E/’Il» (х),
то вместо уравнения (IV.l) получим дифференциальное уравнение моментов
в уравнение (IV.l) кроме искомой величины Т входит так же неизвестная величина Н. То же самое можно сказать и в отношении уравнения (IV.4) , в которое кроме М входит неизвестное Н. Таким образом, необходимо составить еще одно дополнительное уравнение.
Так же, как и в § 2 гл. 111, используем для этой цели принцип Л агранжа, по которому виртуальная работа внешних и внутренних сил кабеля от постоянноЙ нагрузки на перемещениях от временной нагрузки (и температуры) равна нулю:

( Hqds +aIMdS)+ \ g1’J(X) dx=O. J cos ‘f’ Е 1 F cos ‘f’ J

Здесь интегрирование должно распространятся на всю длину нити. Учтя, что d,x
ds=—cos ‘f’
g=-НgУ»(х) Hq=H~Hg, после всех преобразований получим
Ls=!,-l+S1 seC21:1 +S2 sec2 1:2; ОУ•6)
L,=!-l+S1 sec 1:1+S2 sec 1:2′ (IV.7)

Величину ~L определяют по формуле (111.22), а для симметричной нити — по формуле (111.23). Для определения служит формула (111.24).