Трехпролетный мост
Рассмотрим симметричный трехпролетный висячий мост с разрезной балкой жесткости, как показано на рисунке который вы сможете прокомментировать нажав на него мышкой. В общем случае полагаем, что в каждом пролете имеется своя временная нагрузка, расположенная на части балки.
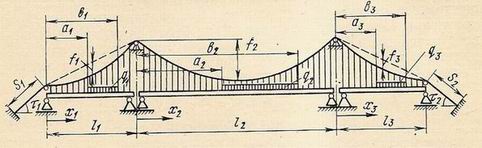
Для каждого пролета примем свои оси координат с началом на левой опоре. Расстояния от левой опоры до произвольного сечения в первом, втором и третьем пролетах, соответственно обозначим через Xj, Х2 и Хз. Точно так же обозначим через a1b1, .а2,Ь2 и азЬз отрезки, определяющие начало и конец загруженного участка в каждом пролёте. Симметрия моста понимается только в геометрическом смысле, нагрузка же может быть расположена, несимметрично.
Для всех функций, которые были введены в предыдущем параграфе, будем принимать прежние обозначения, но к каждой из них добавим по второму индексу, указывающему номер пролета. Например, функция Фl (z) ‘согласно (IV.14) для каждого пролета будет иметь свое значение, а между значениями 21 n 22 существует зависимость 1 ZI=-Z2 2
IV.32
Для значений 11, 11’, М и Q сохраняются все формулы, которые были получены нами в параграфе, только для каждого, пролета должны быть взяты свои значения функций Ф и Р. Существенное отличие будет содержаться в характеристическом уравнении. При составлении его так же будем исходить из основного равенства (JV.5), однако в нем суммирование деформаций должно распространяться на все три пролета. Таким образом, величины Ls и Lt теперь надо определять по. формулам:
Ls = [11[1 + [12[2 + [1iз +51 sec2 ‘»(1 + 52 sec2 ‘»(2;
Lt=~’lt[1 + [12tl2+ [13tlз +51 sec ‘»(1 +52 sec ‘»(2′)
(IV.33)
Значения f.tl, f.t2 И 11з вычисляют по формуле (III.22) а ~tlt, 112t и f.t3t — по формуле (III.24) . Вместо третьего слагаемого во уравнении (IV.5) необходимо взять выражение для трех ,пролётов:
1, 1, 1.
с=у~5111(Х)dх+у;5112(Х)dХ+У;S11з(Х)dХ=- 8~’}
Х [( [;, )’ ~~ J ~1 (x)dx+ ~~, (х) dx+ ( :: )’ {,’ r~, (x)dx 1-
Используя выражение (IV.20), получим 3 ‘ 8/2 g[2 {[1 11 [Q\. ,( ,.1- л (]+ с= —‘ . — —. — -(jilI ZI) — —~I1I ZI) [2 12Н -[2 12 g л
[~~12(Z2)- ~-;:-л ~1I2(Z2)J+~:~: [~~lз-l-;:-Л ~l!3(Zз) Л:
Подстановка в (lV.5) приводит к характеристическому уравнению, которое по форме совпадает с уравнением (IV.23):
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ ДЛЯ ТРЕХПРОЛЕТНОГО МОСТА
Расчет трехпролётного моста состоит из двух частей: решения характеристического уравнения и определения моментов, поперечных сил Н прогибов.
Первая, более сложная, часть состоит в определении величины Л, при которой удовлетворяется характеристическое уравнение (IV.23). Решение провидится путем последовательных приближений по схеме, приведенной выше.
Задаем Н=Лl. Определив па (IV.41), (IV.42), (IV.43) коэффициенты 011(Z), 612(z), 622(Z), ~lР(Z)И ~2P(Z), решаем систему канонических уравнений и находим М1 и М2. Далее по (IV.44) с учетом (IV,45) вычисляем А и В. После этого па (IV.27) определяем Лl и затем новое значение Л2=Лl +~Лl. Процесс повторяется до тех пор, пока 1л не будут меньше заранее заданной величины, предусмотренной желаемой точностью.
Найдя Л, решаем вторую часть, которая сводится, по существу, к вычислениям по Тотовым формулам. Применение современной компьютерной техники позволяет решать задачу по отысканию максимальных моментов и соответствующих им способов загружения моста.
А
-+В-Л=О.
л’